This course introduces Semi-Lagrangian (SL) schemes as a tool for the numerical solution of Hamilton-Jacobi (HJ) equations and optimal control problems. SL schemes are based on the method of characteristics, tracing the flow of information within the equation. An overview of optimal control problems will be presented, including formulations with finite and infinite horizons, the Dynamic Programming Principle, and viscosity solutions.

Numerical methods based on SL schemes will then be illustrated, starting with the linear transport equation and extending the analysis to solving HJ equations.

Le but de ce cours est de donner/rappeler des outils théoriques, les concepts et les algorithmes classiques en optimisation différentiable et non différentiable (avec et sans contraintes), et enfin donner quelques méthodes numériques d'optimisation

Ces séances feront suite au cours introductif sur l'optimisation. Le but étant de pratiquer quelques méthodes numériques d'optimisation.

Le langage Python suffit pour la plupart des besoins en mathématiques appliquées et permet de réaliser beaucoup plus rapidement des programmes informatiques qui fonctionnent sur les principaux systèmes d'exploitation. Le but de ce cours (suivis de TP) étant de donner les principes de bases de ce langage ainsi que ses différentes possibilités pour faire du calcul scientifique, des jeux ou encore des sites Internet moyennant son large panel de librairies.

Le but de ces séances de TP est de pratiquer le langage Python sur des exemples simples afin de toucher ses différentes possibilités de faire du calcul scientifique, des jeux ou encore des sites Internet moyennant son large panel de librairies

Le langage Python suffit pour la plupart des besoins en mathématiques appliquées et permet de réaliser beaucoup plus rapidement des programmes informatiques qui fonctionnent sur les principaux systèmes d'exploitation. Le but de ce cours (suivis de TP) étant de donner les principes de bases de ce langage ainsi que ses différentes possibilités pour faire du calcul scientifique, des jeux ou encore des sites Internet moyennant son large panel de librairies.

Le but de ces séances de TP est de pratiquer le langage Python sur des exemples simples afin de toucher ses différentes possibilités de faire du calcul scientifique, des jeux ou encore des sites Internet moyennant son large panel de librairies

Le but de ce cours est de donner/rappeler des outils théoriques, les concepts et les algorithmes classiques en optimisation différentiable et non différentiable (avec et sans contraintes), et enfin donner quelques méthodes numériques d'optimisation

Ces séances feront suite au cours introductif sur l'optimisation. Le but étant de pratiquer quelques méthodes numériques d'optimisation.

Le but de ce cours est de donner/rappeler des outils théoriques, les concepts et les algorithmes classiques en optimisation différentiable et non différentiable (avec et sans contraintes), et enfin donner quelques méthodes numériques d'optimisation

Ces séances feront suite au cours introductif sur l'optimisation. Le but étant de pratiquer quelques méthodes numériques d'optimisation.

This course introduces Semi-Lagrangian (SL) schemes as a tool for the numerical solution of Hamilton-Jacobi (HJ) equations and optimal control problems. SL schemes are based on the method of characteristics, tracing the flow of information within the equation. An overview of optimal control problems will be presented, including formulations with finite and infinite horizons, the Dynamic Programming Principle, and viscosity solutions.

Numerical methods based on SL schemes will then be illustrated, starting with the linear transport equation and extending the analysis to solving HJ equations.

This course introduces Semi-Lagrangian (SL) schemes as a tool for the numerical solution of Hamilton-Jacobi (HJ) equations and optimal control problems. SL schemes are based on the method of characteristics, tracing the flow of information within the equation. An overview of optimal control problems will be presented, including formulations with finite and infinite horizons, the Dynamic Programming Principle, and viscosity solutions.

Numerical methods based on SL schemes will then be illustrated, starting with the linear transport equation and extending the analysis to solving HJ equations.

This course provides a concise introduction to the theory of gradient flow dynamics in Hilbert spaces and more general metric spaces. We will delve into the fundamental concepts, properties, and applications of gradient flows, exploring their role in understanding the evolution of systems governed by nonlinear PDEs.

Ce cours a pour objectif de présenter une introduction assez complète au thème extrêmement fécond du transport optimal (aussi dit problème de Monge-Kantorovich) et de developper certaines de ses applications. On commencera par étudier quelques cas particuliers (le cas discret, le cas unidimensionnel) puis on introduira la dualité de Kantorovich et montrerons comment en déduire le théorème de Brenier (existence et unicité d'un transport donné par le gradient d'une fonction convexe), nous évoquerons le lien avec les équations de Monge-Ampère et certaines inégalités fonctionnelles. Nous traiterons également le cas d'un coût de transport donné par une distance et sa formulation de type flot minimal à la Beckmann.

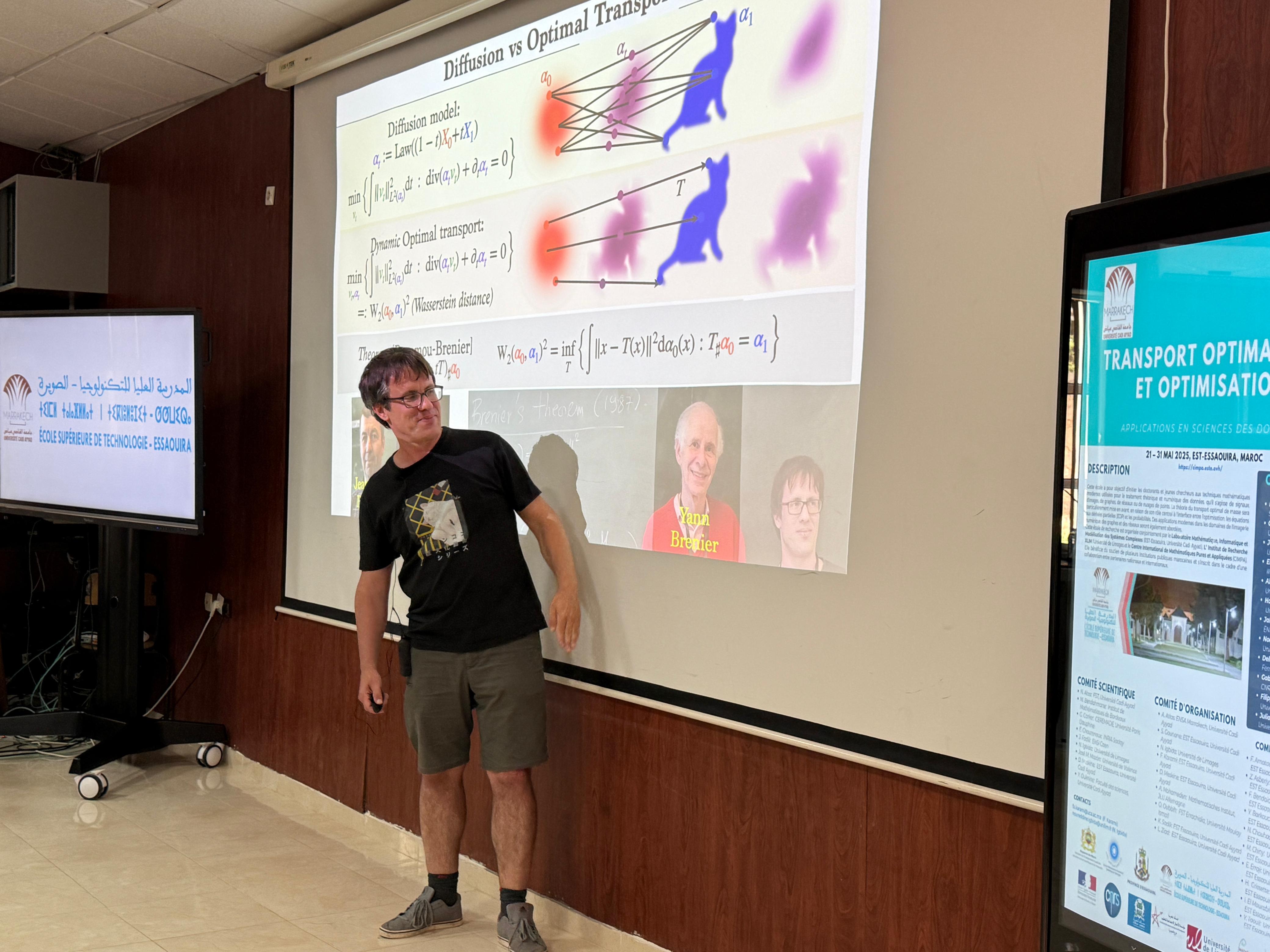
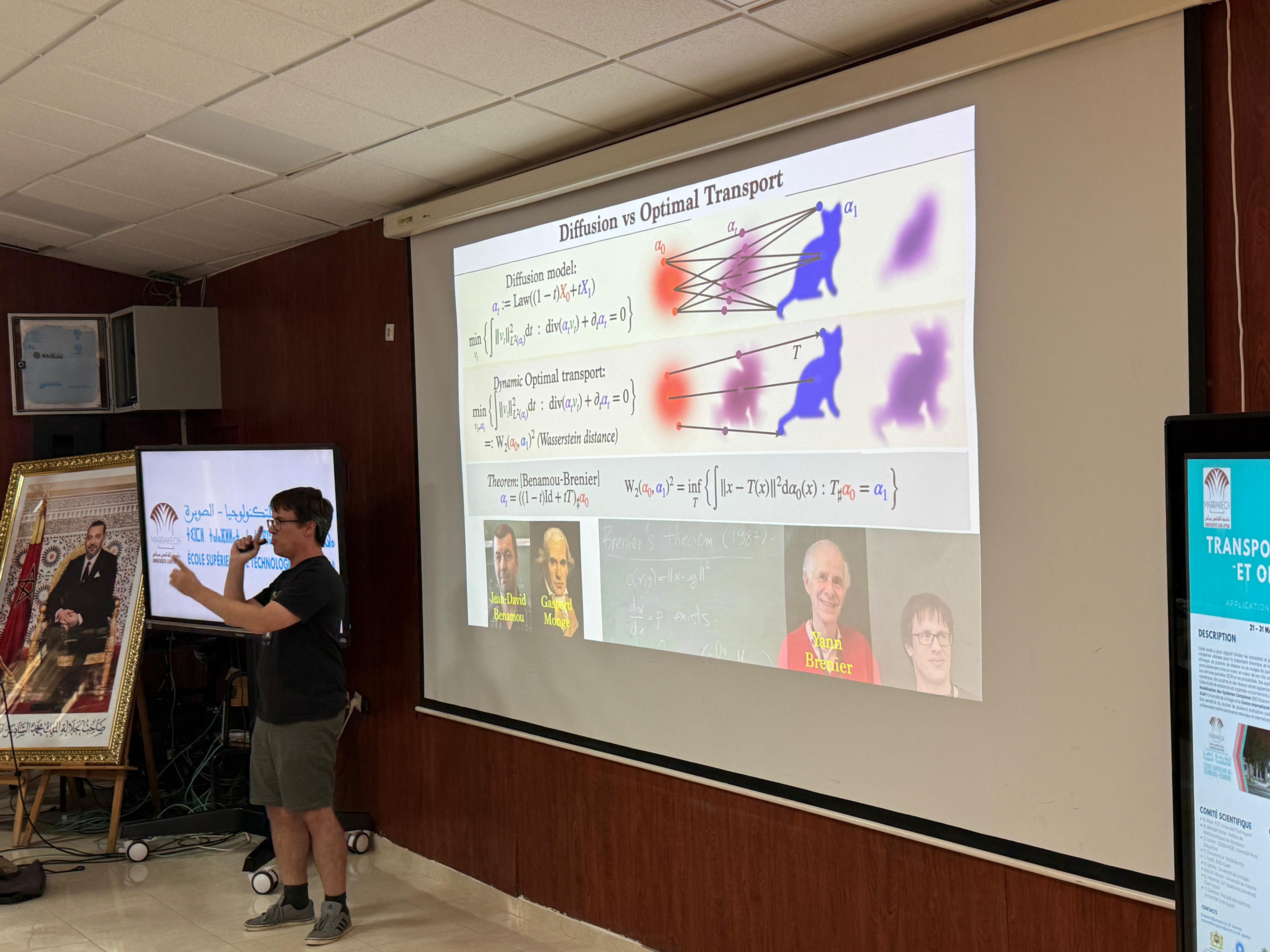
Ce cours fait suite au cours 1. Nous aborderons ici la formulation dynamique (Benamou-Brenier) du transport optimal, ce qui fera un pont naturel avec les méthodes de transport pour les équations d'évolution notamment les flots de gradients dans l'espace de Wasserstein. Nous évoquerons enfin le lien entre transport optimal et dynamique des fluides incompressibles

Ce cours fait suite au cours 1. Nous aborderons ici la formulation dynamique (Benamou-Brenier) du transport optimal, ce qui fera un pont naturel avec les méthodes de transport pour les équations d'évolution notamment les flots de gradients dans l'espace de Wasserstein. Nous évoquerons enfin le lien entre transport optimal et dynamique des fluides incompressibles

Ce cours a pour objectif de présenter une introduction assez complète au thème extrêmement fécond du transport optimal (aussi dit problème de Monge-Kantorovich) et de developper certaines de ses applications. On commencera par étudier quelques cas particuliers (le cas discret, le cas unidimensionnel) puis on introduira la dualité de Kantorovich et montrerons comment en déduire le théorème de Brenier (existence et unicité d'un transport donné par le gradient d'une fonction convexe), nous évoquerons le lien avec les équations de Monge-Ampère et certaines inégalités fonctionnelles. Nous traiterons également le cas d'un coût de transport donné par une distance et sa formulation de type flot minimal à la Beckmann.

Le transport optimal (OT) est une théorie mathématique à l'interface entre l'optimisation, les équations aux dérivées partielles et les probabilités. Il est récemment apparu comme un outil important pour traiter une gamme étonnamment large de problèmes applicatifs, tels que la mise en correspondance de formes en imagerie médicale, les problèmes de prédiction structurée en apprentissage supervisé et l'entrainement de réseaux génératifs profonds. Dans ce cours, je ferai un tour d'horizon depuis la description de la théorie mathématique jusqu'aux développements récents des solveurs numériques qui permettent de passer à l'échelle. J'insisterai en particulier sur l’importance des récents progrès obtenus par des approches par régularisation entropique, qui permettent de s’attaquer aux problèmes d’apprentissage en grandes dimensions. Plus d'information sont disponibles en ligne via https://optimaltransport.github.io/

Le but de ces séances étant de présenter et illustrer à l'aide de simulations numériques certains exemples abordés dans le cours avancé "transport optimal computationnel".

Le transport optimal (OT) est une théorie mathématique à l'interface entre l'optimisation, les équations aux dérivées partielles et les probabilités. Il est récemment apparu comme un outil important pour traiter une gamme étonnamment large de problèmes applicatifs, tels que la mise en correspondance de formes en imagerie médicale, les problèmes de prédiction structurée en apprentissage supervisé et l'entrainement de réseaux génératifs profonds. Dans ce cours, je ferai un tour d'horizon depuis la description de la théorie mathématique jusqu'aux développements récents des solveurs numériques qui permettent de passer à l'échelle. J'insisterai en particulier sur l’importance des récents progrès obtenus par des approches par régularisation entropique, qui permettent de s’attaquer aux problèmes d’apprentissage en grandes dimensions. Plus d'information sont disponibles en ligne via https://optimaltransport.github.io/

Le but de ces séances étant de présenter et illustrer à l'aide de simulations numériques certains exemples abordés dans le cours avancé "transport optimal computationnel".

This mini-course offers a comprehensive exploration of linear diffusion equations on metric graphs. In my lectures I will delve into four key topics:

• Heat Kernels and Qualitative Properties: A foundational understanding of heat kernels and their associated properties, such as smoothness and pointwise bounds.
• Variational Methods and Convergence: The application of variational techniques to analyze the rate of convergence to equilibrium and the effectiveness of thermal insulation.
• Shape Optimization: An examination of shape optimization problems for metric graphs, focusing on both heat content and heat trace.
• Non-Standard Boundary Conditions and Higher-Order Operators: The extension of our analysis to non-standard boundary conditions and higher-order elliptic operators, introducing the concept of eventually Markovian behavior.

L'optimisation, en particulier non-lisse, est omniprésente dans les méthodes moderne de traitement et d'analyse de données (signal, image, graphe, nuage de points, etc.), ainsi qu'en apprentissage statistique. En effet, l'immense majorité des problèmes dans ces domaines d'application se ramènent à l'optimisation d'une fonctionnelle non-lisse mais structurée, possiblement non-convexe, en très grande dimension (voire en dimension infinie). Ce cours fournira les outils nécessaires en analyse et optimisation non-lisses pour résoudre de tels problèmes d'optimisation en tirant parti de leur structure. On décrira à la fois les outils mathématique sous-jacents, les algorithmes, ainsi que leurs garanties théoriques notamment de convergence. On se focalisera en particulier sur les algorithmes dits d'éclatement d'opérateurs. Des séances de travaux pratiques seront consacrés à l'implémentation de ces algorithmes.

Ces séances de travaux pratiques, relatives au cours "Optimisation en traitement des données", seront consacrées à l'implémentation de certains algorithmes, notamment les algorithmes dits d'éclatement d'opérateurs.

L'optimisation, en particulier non-lisse, est omniprésente dans les méthodes moderne de traitement et d'analyse de données (signal, image, graphe, nuage de points, etc.), ainsi qu'en apprentissage statistique. En effet, l'immense majorité des problèmes dans ces domaines d'application se ramènent à l'optimisation d'une fonctionnelle non-lisse mais structurée, possiblement non-convexe, en très grande dimension (voire en dimension infinie). Ce cours fournira les outils nécessaires en analyse et optimisation non-lisses pour résoudre de tels problèmes d'optimisation en tirant parti de leur structure. On décrira à la fois les outils mathématique sous-jacents, les algorithmes, ainsi que leurs garanties théoriques notamment de convergence. On se focalisera en particulier sur les algorithmes dits d'éclatement d'opérateurs. Des séances de travaux pratiques seront consacrés à l'implémentation de ces algorithmes.

Ces séances de travaux pratiques, relatives au cours "Optimisation en traitement des données", seront consacrées à l'implémentation de certains algorithmes, notamment les algorithmes dits d'éclatement d'opérateurs.

L'optimisation, en particulier non-lisse, est omniprésente dans les méthodes moderne de traitement et d'analyse de données (signal, image, graphe, nuage de points, etc.), ainsi qu'en apprentissage statistique. En effet, l'immense majorité des problèmes dans ces domaines d'application se ramènent à l'optimisation d'une fonctionnelle non-lisse mais structurée, possiblement non-convexe, en très grande dimension (voire en dimension infinie). Ce cours fournira les outils nécessaires en analyse et optimisation non-lisses pour résoudre de tels problèmes d'optimisation en tirant parti de leur structure. On décrira à la fois les outils mathématique sous-jacents, les algorithmes, ainsi que leurs garanties théoriques notamment de convergence. On se focalisera en particulier sur les algorithmes dits d'éclatement d'opérateurs. Des séances de travaux pratiques seront consacrés à l'implémentation de ces algorithmes.

Ces séances de travaux pratiques, relatives au cours "Optimisation en traitement des données", seront consacrées à l'implémentation de certains algorithmes, notamment les algorithmes dits d'éclatement d'opérateurs.

Récemment, l’adaptation et la résolution des EDP portant sur des données fournies par des graphes et des réseaux arbitraires ont suscité un vif intérêt. Afin de traduire et de résoudre les EDP sur des graphes, différents calculs vectoriels discrets ont été proposés dans la littérature ces dernières années. Un calcul discret simple sur des graphes est basé sur des différences partielles discrètes, ce qui permet de résoudre des EDP sur des domaines de données réguliers ou irréguliers d’une manière simple et unifiée. Cette approche mimétique consiste à remplacer les opérateurs différentiels partiels continus, par exemple, les gradients ou les divergences, par un analogue discret raisonnable, ce qui permet de transférer de nombreux outils et résultats importants à partir du réglage continu. Ce cours a pour objectif de proposer une introduction complète aux méthodes numériques de type EDP sur des graphes et leurs applications en traitement de l'image, du signal et des données, et en apprentissage automatique.

Cette session commencera par des séances de TP qui illustrerontle cours introductif sur le traitement de données et graphe, et qui permettront aux étudiants de manipuler et traiter de données pour des exemples simples. Le reste des séances se réfère aux cours avancé ''EDP sur graphes et applications '' et se focalisera sur la manipulation des méthodes de type EDP pour le traitement de quelques exemples concrets en image, signal et données, et en apprentissage automatique.

This mini-course offers a comprehensive exploration of linear diffusion equations on metric graphs. In my lectures I will delve into four key topics:

• Heat Kernels and Qualitative Properties: A foundational understanding of heat kernels and their associated properties, such as smoothness and pointwise bounds.
• Variational Methods and Convergence: The application of variational techniques to analyze the rate of convergence to equilibrium and the effectiveness of thermal insulation.
• Shape Optimization: An examination of shape optimization problems for metric graphs, focusing on both heat content and heat trace.
• Non-Standard Boundary Conditions and Higher-Order Operators: The extension of our analysis to non-standard boundary conditions and higher-order elliptic operators, introducing the concept of eventually Markovian behavior.

This mini-course offers a comprehensive exploration of linear diffusion equations on metric graphs. In my lectures I will delve into four key topics:

• Heat Kernels and Qualitative Properties: A foundational understanding of heat kernels and their associated properties, such as smoothness and pointwise bounds.
• Variational Methods and Convergence: The application of variational techniques to analyze the rate of convergence to equilibrium and the effectiveness of thermal insulation.
• Shape Optimization: An examination of shape optimization problems for metric graphs, focusing on both heat content and heat trace.
• Non-Standard Boundary Conditions and Higher-Order Operators: The extension of our analysis to non-standard boundary conditions and higher-order elliptic operators, introducing the concept of eventually Markovian behavior.

We will study different diffusion problems in the workspace of metric random walk spaces, which include particularly discrete weighted graphs, and different aspects related to the operators involved in such problems. For example, we will study a ROF model and the corresponding gradient descent method in metric random walk spaces, which involves the study of the 1-Laplacian in such spaces.

We will study different diffusion problems in the workspace of metric random walk spaces, which include particularly discrete weighted graphs, and different aspects related to the operators involved in such problems. For example, we will study a ROF model and the corresponding gradient descent method in metric random walk spaces, which involves the study of the 1-Laplacian in such spaces.

Récemment, l’adaptation et la résolution des EDP portant sur des données fournies par des graphes et des réseaux arbitraires ont suscité un vif intérêt. Afin de traduire et de résoudre les EDP sur des graphes, différents calculs vectoriels discrets ont été proposés dans la littérature ces dernières années. Un calcul discret simple sur des graphes est basé sur des différences partielles discrètes, ce qui permet de résoudre des EDP sur des domaines de données réguliers ou irréguliers d’une manière simple et unifiée. Cette approche mimétique consiste à remplacer les opérateurs différentiels partiels continus, par exemple, les gradients ou les divergences, par un analogue discret raisonnable, ce qui permet de transférer de nombreux outils et résultats importants à partir du réglage continu. Ce cours a pour objectif de proposer une introduction complète aux méthodes numériques de type EDP sur des graphes et leurs applications en traitement de l'image, du signal et des données, et en apprentissage automatique.

Cette session commencera par des séances de TP qui illustrerontle cours introductif sur le traitement de données et graphe, et qui permettront aux étudiants de manipuler et traiter de données pour des exemples simples. Le reste des séances se réfère aux cours avancé ''EDP sur graphes et applications '' et se focalisera sur la manipulation des méthodes de type EDP pour le traitement de quelques exemples concrets en image, signal et données, et en apprentissage automatique.

Récemment, l’adaptation et la résolution des EDP portant sur des données fournies par des graphes et des réseaux arbitraires ont suscité un vif intérêt. Afin de traduire et de résoudre les EDP sur des graphes, différents calculs vectoriels discrets ont été proposés dans la littérature ces dernières années. Un calcul discret simple sur des graphes est basé sur des différences partielles discrètes, ce qui permet de résoudre des EDP sur des domaines de données réguliers ou irréguliers d’une manière simple et unifiée. Cette approche mimétique consiste à remplacer les opérateurs différentiels partiels continus, par exemple, les gradients ou les divergences, par un analogue discret raisonnable, ce qui permet de transférer de nombreux outils et résultats importants à partir du réglage continu. Ce cours a pour objectif de proposer une introduction complète aux méthodes numériques de type EDP sur des graphes et leurs applications en traitement de l'image, du signal et des données, et en apprentissage automatique.

Cette session commencera par des séances de TP qui illustrerontle cours introductif sur le traitement de données et graphe, et qui permettront aux étudiants de manipuler et traiter de données pour des exemples simples. Le reste des séances se réfère aux cours avancé ''EDP sur graphes et applications '' et se focalisera sur la manipulation des méthodes de type EDP pour le traitement de quelques exemples concrets en image, signal et données, et en apprentissage automatique.

We will study different diffusion problems in the workspace of metric random walk spaces, which include particularly discrete weighted graphs, and different aspects related to the operators involved in such problems. For example, we will study a ROF model and the corresponding gradient descent method in metric random walk spaces, which involves the study of the 1-Laplacian in such spaces.